우리가치 모각코 5회차

1. 일시
👉🏻 2022년 10월 28일
2. 장소
👉🏻 성곡도서관 지하 1층 카페 인피니티 / 공학관 카페
3. 학습내용
오늘은 각자 풀고 싶은 알고리즘 문제를 정하고, 풀어보는 시간을 갖었다.
#11444
내가 정한 문제는 11444번의 피보나치 수 6 문제였다.
피보나치 수는 첫 번째 항과 두 번째 항은 1이고, 그 다음 항부터는 현재 항의 값이 전전항과 전항의 합인 수열이라 알고 있었다. 그래서 피보나치 수를 구하기 위한 방법은 앞에서부터 하나씩 더하는 방식 하나만 존재한다고 생각했었는데, 행렬의 거듭제곱으로 구하는 방법이 있다는 것을 알게 되었다. 그런데 이러한 방법을 이용하여 코드로 구현하는 것이 어려워, 여러 도움을 받아 이해하고 풀 수 있었다.
내가 다시 이해하면서, 코드를 최적화시키며 작성해 볼 필요성을 느꼈다.
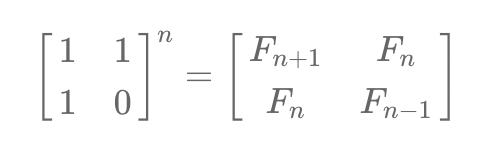
#include <iostream>
#define MOD 1000000007
using namespace std;
typedef long long ll;
ll N;
ll f[2][2] = {{1, 1}, {1, 0}};
ll base[2][2] = {{1, 1}, {1, 0}};
void matmul_self()
{
ll x1 = (((f[0][0] * f[0][0]) % MOD) + ((f[0][1] * f[1][0]) % MOD)) % MOD;
ll y1 = (((f[0][0] * f[0][1]) % MOD) + ((f[0][1] * f[1][1]) % MOD)) % MOD;
ll x2 = (((f[1][0] * f[0][0]) % MOD) + ((f[1][1] * f[1][0]) % MOD)) % MOD;
ll y2 = (((f[1][0] * f[0][1]) % MOD) + ((f[1][1] * f[1][1]) % MOD)) % MOD;
f[0][0] = x1;
f[0][1] = y1;
f[1][0] = x2;
f[1][1] = y2;
}
void matmul_base()
{
ll x1 = (((f[0][0] * base[0][0]) % MOD) + ((f[0][1] * base[1][0])) % MOD) % MOD;
ll y1 = (((f[0][0] * base[0][1]) % MOD) + ((f[0][1] * base[1][1])) % MOD) % MOD;
ll x2 = (((f[1][0] * base[0][0]) % MOD) + ((f[1][1] * base[1][0])) % MOD) % MOD;
ll y2 = (((f[1][0] * base[0][1]) % MOD) + ((f[1][1] * base[1][1])) % MOD) % MOD;
f[0][0] = x1;
f[0][1] = y1;
f[1][0] = x2;
f[1][1] = y2;
}
void fibonacci(ll n)
{
if (n <= 1)
{
return;
}
fibonacci(n / 2);
matmul_self();
if (n % 2 == 1)
{
matmul_base();
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> N;
if (N == 0)
{
cout << 0 << "\n";
return 0;
}
else if (N == 1)
{
cout << 1 << "\n";
return 0;
}
fibonacci(N);
cout << f[0][1] % MOD << "\n";
return 0;
}4. 소감(느낀 점)
중간고사 끝나고, 오랜만에 모각코를 진행하였다. 서로 시간표가 다른 탓에 강의 듣는 건물까지 달라, 모각코가 아니면 자주 모이지 못했는데, 이렇게 모각코를 통해 얼굴도 보고 공부도 같이 할 수 있어 하루를 잘 마무리 하는 것 같아 기분이 좋았다. 남은 회차도 열심히 으쌰으쌰할 수 있으면..😊!
https://www.acmicpc.net/problem/11444
11444번: 피보나치 수 6
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
우리가치 모각코 5회차

1. 일시
👉🏻 2022년 10월 28일
2. 장소
👉🏻 성곡도서관 지하 1층 카페 인피니티 / 공학관 카페
3. 학습내용
오늘은 각자 풀고 싶은 알고리즘 문제를 정하고, 풀어보는 시간을 갖었다.
#11444
내가 정한 문제는 11444번의 피보나치 수 6 문제였다.
피보나치 수는 첫 번째 항과 두 번째 항은 1이고, 그 다음 항부터는 현재 항의 값이 전전항과 전항의 합인 수열이라 알고 있었다. 그래서 피보나치 수를 구하기 위한 방법은 앞에서부터 하나씩 더하는 방식 하나만 존재한다고 생각했었는데, 행렬의 거듭제곱으로 구하는 방법이 있다는 것을 알게 되었다. 그런데 이러한 방법을 이용하여 코드로 구현하는 것이 어려워, 여러 도움을 받아 이해하고 풀 수 있었다.
내가 다시 이해하면서, 코드를 최적화시키며 작성해 볼 필요성을 느꼈다.
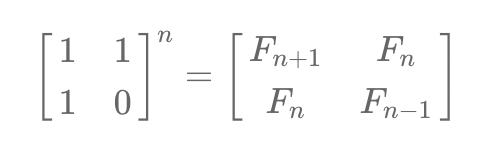
#include <iostream>
#define MOD 1000000007
using namespace std;
typedef long long ll;
ll N;
ll f[2][2] = {{1, 1}, {1, 0}};
ll base[2][2] = {{1, 1}, {1, 0}};
void matmul_self()
{
ll x1 = (((f[0][0] * f[0][0]) % MOD) + ((f[0][1] * f[1][0]) % MOD)) % MOD;
ll y1 = (((f[0][0] * f[0][1]) % MOD) + ((f[0][1] * f[1][1]) % MOD)) % MOD;
ll x2 = (((f[1][0] * f[0][0]) % MOD) + ((f[1][1] * f[1][0]) % MOD)) % MOD;
ll y2 = (((f[1][0] * f[0][1]) % MOD) + ((f[1][1] * f[1][1]) % MOD)) % MOD;
f[0][0] = x1;
f[0][1] = y1;
f[1][0] = x2;
f[1][1] = y2;
}
void matmul_base()
{
ll x1 = (((f[0][0] * base[0][0]) % MOD) + ((f[0][1] * base[1][0])) % MOD) % MOD;
ll y1 = (((f[0][0] * base[0][1]) % MOD) + ((f[0][1] * base[1][1])) % MOD) % MOD;
ll x2 = (((f[1][0] * base[0][0]) % MOD) + ((f[1][1] * base[1][0])) % MOD) % MOD;
ll y2 = (((f[1][0] * base[0][1]) % MOD) + ((f[1][1] * base[1][1])) % MOD) % MOD;
f[0][0] = x1;
f[0][1] = y1;
f[1][0] = x2;
f[1][1] = y2;
}
void fibonacci(ll n)
{
if (n <= 1)
{
return;
}
fibonacci(n / 2);
matmul_self();
if (n % 2 == 1)
{
matmul_base();
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> N;
if (N == 0)
{
cout << 0 << "\n";
return 0;
}
else if (N == 1)
{
cout << 1 << "\n";
return 0;
}
fibonacci(N);
cout << f[0][1] % MOD << "\n";
return 0;
}4. 소감(느낀 점)
중간고사 끝나고, 오랜만에 모각코를 진행하였다. 서로 시간표가 다른 탓에 강의 듣는 건물까지 달라, 모각코가 아니면 자주 모이지 못했는데, 이렇게 모각코를 통해 얼굴도 보고 공부도 같이 할 수 있어 하루를 잘 마무리 하는 것 같아 기분이 좋았다. 남은 회차도 열심히 으쌰으쌰할 수 있으면..😊!
https://www.acmicpc.net/problem/11444
11444번: 피보나치 수 6
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
